🖱️관계형 데이터베이스 : 2차원적인 표(table)를 이용해서 데이터 상호 관계를 정의하는 데이터베이스
- 1970년 IBM에 근무하던 코드(E.F.Code)에 의해 처음 제안
- 개체(entity)와 관계(relationship)를 모두 릴레이션(relation)이라는 표(table)로 표현하기때문에 개체를 개체 릴레이션과 관계 릴레이션이 존재
- 장점 : 간결하고 보기 편리하며, 다른 데이터베이스로의 변환이 용이
- 단점 : 성능이 다소 떨어짐
🖱️관계형 데이터베이스의 구조 :
- 릴레이션(relation) : 데이터들을 표(table)의 형태로 표현한 것으로, 구조를 나타내는 릴레이션 스키마와 실제 값들은 릴레이션 인스턴스로 구성
<학생> 릴레이션
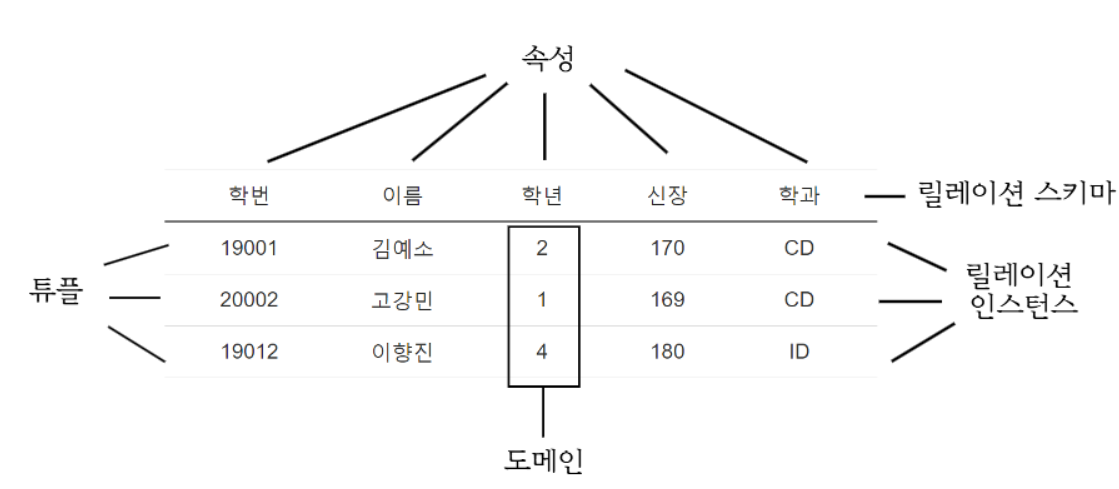
- 튜플(tuple) : 릴레이션을 구성하는 각각의 행 / 속성 모임으로 구성 / 파일 구조에서 레코드와 같은 의미 / 튜플의 수를 카디널리티(cardinality) 또는 기수, 대응수라고 함
- 속성(attribute) : 데이터베이스를 구성하는 가장 작은 논리적 단위 / 파일 구조상 데이터 항목 또는 데이터 필드에 해당 / 개체의 특성을 기술 / 속성의 수를 디그리(degree) 또는 차수라고 함
- 도메인(domain) : 하나의 애트리뷰트가 취할 수 있는 같은 타입의 원자(atomic)값들의 집합 / 값의 합법 여부를 시스템이 검사하는 데에도 이용
- 릴레이션의 특징 :
1. 똑같은 튜플이 포함될 수 없음
2. 튜플 사이에는 순서가 없음
3. 튜플의 삽입, 삭제 등의 작업으로 릴레이션은 시간에 따라 변함
4. 스키마를 구성하는 속성들 간의 순서는 중요하지 않음
5. 속성의 유일한 식별을 위해 속성의 명칭은 유일해야 하지만, 값은 동일한 값이 있을 수 있음
6. 튜플을 유일하게 식별하기 위해 속성들의 부분집합을 키(key)로 설정함
7. 속성의 값은 논리적으로 더 이상 쪼개질 수 없는 원자값만을 저장
🖱️관계형 데이터베이스 모델(ralational data model) : 2차원적인 표(table)를 이용해 데이터 상호 관계를 정의하는 DB구조
- 가장 널리 사용되는 데이터 모델
- 파일 구조처럼 구성한 테이블들을 하나의 DB로 묶어서 테이블 내에 있는 속성들 간의 관계(relationship)를 설정하거나 테이블 간의 관계를 설정하여 이용
- 기본키(primary key)와 이를 참조하는 외래키(foreign key)로 데이터 간의 관계를 표현
- 계층 모델과 망 모델의 복잡한 구조를 단순화시킨 모델
- 관계형 모델의 대표적인 언어는 SQL
- 1:1, 1:N, N:M 관계를 자유롭게 표현가능
🖱️관계형 데이터베이스의 제약조건 - 키(key) : 데이터베이스에서 조건에 만족하는 튜플을 찾거나 순서대로 정렬할 때 기준이 되는 속성
- 키의 종류 : 후보키(candidate key), 기본키(primary key), 대체키(alternate key), 슈퍼키(super key), 외래키(foreign key)
⌨️ 후보키(candidate key) : 릴레이션을 구성하는 속성 중 튜플을 유일하게 식별하기 위해 사용되는 속성들의 부분집합
- 기본키로 사용할 수 있는 속성들을 말함
- 유일성과 최소성을 모두 만족시켜야 함
- 유일성(unique) : 하나의 키 값으로 하나의 튜플만을 유일하게 식별할 수 있어야 함
- 최소성(minimality) : 키를 구성하는 속성 하나를 제거하면 유일하게 식별할 수 없도록 꼭 필요한 최소의 속성으로 구성
⌨️ 기본키(primary key) : 후보키 중에서 특별히 선정된 주키(main key)
- 중복된 값을 가질 수 없음
- 한 릴레이션에서 특정 튜플을 유일하게 구별할 수 있는 속성
- NULL값을 가질 수 없음
⌨️ 대체키(alternate key) : 후보키가 둘 이상일 때 기본키를 제외한 나머지 후보키(a.k.a. 보조키)
⌨️ 슈퍼키(super key) : 한 릴레이션 내에 있는 속성들의 집합으로 구성된 키
- 릴레이션을 구성하는 모든 튜플 중 슈퍼키로 구성된 속성의 집합 과 동일한 값은 나타나지 않음
- 유일성은 만족하지만 최소성은 만족하지 못함
⌨️ 외래키(foreign key) : 다른 링레이션의 기본키를 참조하는 속성 또는 속성들의 집합
- 한 릴레이션에 속한 속성 A와 참조 릴레이션의 기본키인 B가 동일한 도메인 상에서 정의되었을 때 속성 A = 외래키
- 외래키로 지정되면 참조 릴레이션의 기본키에 없는 값은 입력할 수 없음
ex)
| 학번 | 이름 | 주민번호 | 전화 |
| 001 | 홍XX | 95XXXX-XXXXXXX | 010-XXXX-XXXX |
| 002 | 김XX | 98XXXX-XXXXXXX | 010-XXXX-XXXX |
| 003 | 이XX | 00XXXX-XXXXXXX | 010-XXXX-XXXX |
| 004 | 김XX | 93XXXX-XXXXXXX | 010-XXXX-XXXX |
| 학번 | 과목명 |
| 001 | 영어 |
| 001 | 수학 |
| 002 | 영어 |
| 003 | 국어 |
| 004 | 과학 |
후보키 : 학번, 주민번호
기본키: 학번(선정)
대체키 : 주민번호
슈퍼키 : ex) 이름+주민번호 ...
외래키 : 학번
🖱️관계형 데이터베이스의 제약조건 - 무결성(integrity) : 데이터베이스에 저장된 데이터 값과 그것이 표현하는 현실 세계의 실제값이 일치하는 정확성을 의미
- 무결성 제약 조건 : 데이터베이스에 들어 있는 데이터의 정확성을 보장하기 위해 부정확한 자료가 데이터베이스 내에 저장되는 것을 방지하기 위한 제약소전을 말함
- 종류 :
| 개체 무결성** | 기본 테이블의 기본키를 구성하는 어떤 속성도 Null값이나 중복값을 가질 수 없음 |
| 참조 무결성** | 외래키 값은 Null이거나 참조 릴레이션의 기본키 값과 동일해야함 |
| 도메인 무결성 | 주어진 속성 값이 정의된 도메인에 속한 값이어야 함 |
| 사용자 정의 무결성 | 속성 값들이 사용자가 정의한 제약조건에 만족되어야 함 |
| NULL 무결성 | 릴레이션의 특정 속성값이 NULL이 될 수 없음 |
| 고유 무결성 | 릴레이션의 특정 속성에 대해 각 튜플이 갖는 속성값들이 서로 달라야 함 |
| 키 무결성 | 하나의 릴레이션에는 적어도 하나의 키가 존재해야 함 |
| 관계 무결성 | 릴레이션에 어느 한 튜플의 삽입 가능 여부, 또는 한 릴레이션과 다른 릴레이션의 튜플들 사이의 관계에 대한 적절성 여부를 지정한 규정 |
- 데이터 무결성 강화 : 데이터 무결성은 데이터 품질에 직접적인 영향을 미치므로 데이터 특성에 맞는 적절한 무결성을 정의하고 강화해야 함
| 강화방법 | |
| 애플리케이션 | 데이터 생성, 수정, 삭제 시 무결성 조건을 검증하는 코드를 프로그램 내에 추가 |
| 데이터베이스 트리거 | 트리거 이벤트에 무결성 조건을 실행하는 절차형 SQL을 추가 |
| 제약 조건 | 데이터베이스에 제약 조건을 설정하여 무결성을 유지 |
🖱️관계대수 : 관계형 데이터베이스에서 원하는 정보와 그 정보를 검색하기 위해서 어떻게 유도하는 가를 기술하는 절차적 언어
- 릴레이션을 처리하기 위해 연산자와 연산규칙을 제공, 피연산자와 연산 결과가 모두 릴레이션
- 질의에 대한 해를 구하기 위해 수행해야 할 연산의 순서 명시
- 특별히 개발한 순수 관계 연산자와 수학적 집합 이론에서 사용하는 일반 집합 연산자가 있음
| 순수 관계 연산자 | ||
| select | - 릴레이션에 존재하는 튜플 중에서 선택 조건을 만족하는 튜플의 부분집합을 구하여 새로운 릴레이션을 만드는 연산 - 릴레이션의 행에 해당하는 튜플을 구현하는 것이므로 수평 연산이라고도 함 |
σ (시그마) |
| project | - 주어진 릴레이션에서 속성 리스트(attribute list)에 제시된 속성 값만을 추출하여 새로운 릴레이션을 만드는 연산 - 연산 결과에 중복이 발생하면 중복이 제거됨 - 릴레이션의 열에 해당하는 속성을 추출하는 것이므로 수직 연산자라고도 함 |
π (파이) |
| join | - 공통 속성을 중심으로 두 개의 릴레이션을 하나로 합쳐서 새로운 릴레이션을 만드는 연산 - join의 결과는 cartesian product(교차곱)을 수행한 다음 select를 수행한 것과 같음 |
▷◁ |
| division | - X ⊃ Y인 두 개의 릴레이션 R(X) 와 S(Y)가 있을 때, R의 속성이 S의 속성값을 모두 가진 튜플에서 S가 가진 속성을 제외한 속성만을 구하는 연산 | ÷ |
| 일반 집합 연산자 | - 수학적 집합 이론에서 사용하는 연산자 - 합집합, 교집합, 차집합을 처리하기 위해 합병 조건을 만족해야 함 - 합병 가능한 두 릴레이션 R과 S가 있을 때 각 연산의 특징을 요약하면 다음과 같음 |
|
| 합집합 (UNION) ∪ |
- 두 릴레이션에 존재하는 튜플의 합집합을 구하되, 결과로 생성된 릴레이션에서 중복되는 튜플은 제거되는 연산 - R ∪ S = {t|t ∈ R ⋁ t ∈ S} * t는 릴레이션 R 또는 S에 존재하는 튜플 |
- |R ∪ S| ≤ |R| + |S| - 합집합의 카디널리티(튜플의 수)는 두 릴레이션 카디널리티의 합보다 크지 않음 |
| 교집합 (INTERSECTION) ∩ |
- 두 릴레이션에 존재하는 튜플의 교집합을 구하는 연산 - R ∩ S = {t|t ∈ R ⋀ t ∈ S} * t는 릴레이션 R 그리고 S에 동시에 존재하는 튜플 |
- |R ∩ S| ≤ MIN{ |R| , |S| } - 교집합의 카디널리티는 두 릴레이션 중 카디널리티가 적은 릴레이션의 카디널리티보다 크지 않음 |
| 차집합 (DIFFERENCE) - |
- 두 릴레이션에 존재하는 튜플의 차집합을 구하는 연산 - R - S = {t|t ∈ R ⋀ t ∉ S} * t는 릴레이션 R에는 존재하고 S에는 존재하지 않는 튜플 |
- |R - S| ≤ |R| - 차집합의 카디널리티는 릴레이션 R의 카디널리티보다 크지 않음 |
| 교차곱 (CARTESIAN PRODUCT) x |
- 두 릴레이션에 있는 튜플들의 순서 쌍을 구하는 연산 - R x S = {r • s| r ∈ R ⋀ s ∈ S} * r은 R에 존재하는 튜플이고, s는 S에 존재하는 튜플 |
- |R x S| = |R| x |S| - 교차곱은 두 릴레이션의 카디널리티를 곱한 것과 같음 |
🖱️관계해석 : 관계데이터의 연산을 표현하는 방법
- 관계 데이터 모델의 제안자인 코드(E.F. Codd)가 수학의 Predicate Calculus(술어 해석)에 기반을 두고 관계 데이터베이스를 위해 제안했음
- 원하는 정보가 무엇이라는 것만 정의하는 비절차적 특성을 지님
- 원하는 정보를 정의할 때는 계산 수식을 사용
* 관계대수 : 어떻게 데이터를 조회할지 정의
* 관계해석 : 원하는 정보가 무엇인지 정의
[시나공 정보처리기사] 실기 토막강의
[기출문제 사이트]
